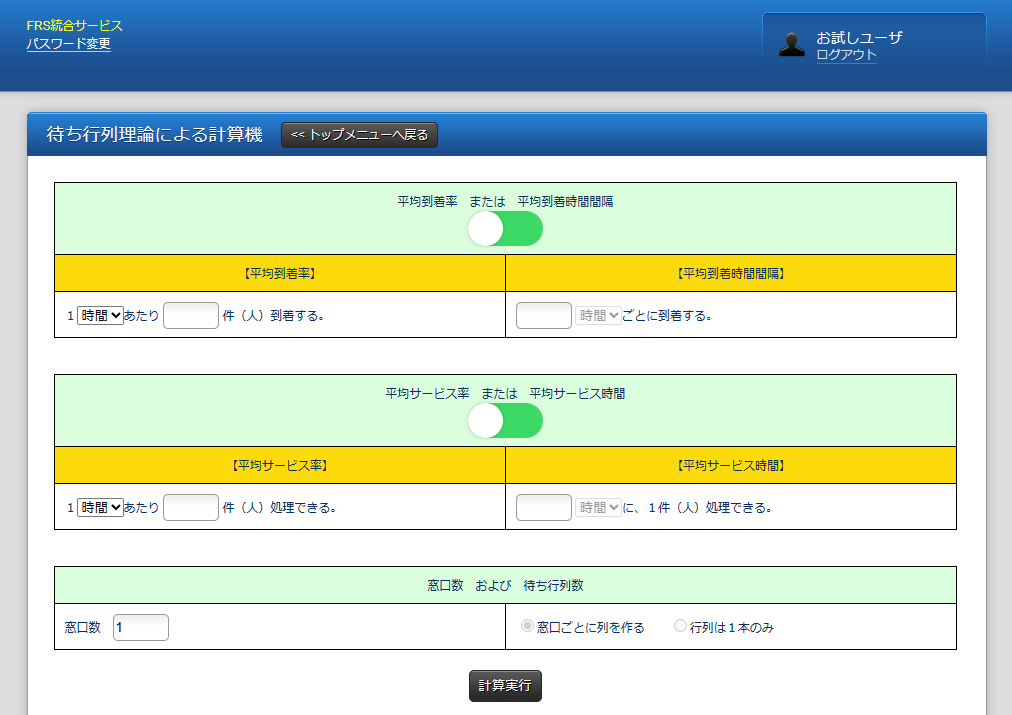
待ち行列理論に基づく待ち時間計算ツール
【M/M/1】と【M/M/m(m≧2)】の二つをWeb上で簡単に計算可能です。
また訳の分からないことを…とお思いでしょうが、世の中に存在する様々な行列(マトリックスではなくキュー)に適用できる考え方です。
そう、コンビニやスーパーのレジ待ちの行列、有名飲食店の店外にできる行列、銀行のATMコーナーに生じる行列等、様々な行列が存在しますが、それらの行列の待ち時間をあらかじめ推測できるということは適切なサービス窓口の設計(レジをいくつ設置するのか等)に活用できるのです。
さらに銀行のATMコーナーにおいて、その多くが昼休みの時間にロープを張ることでお客様の並ぶ列を1本にしています。その理由は何なのでしょうか?
ATMが5台あると仮定して、ATMごとに並ばせる(列は5本)のと、列を1本にする場合を比較してみます。ATMを利用する時間もお客様の来る頻度も変わらないにもかかわらず、お客様の待ち時間が劇的に減少することが確率的に分かっているのです。不思議ですね。
【M/M/1】が5つ(ATM5台、列はATMごと)と【M/M/5】が1つ(ATM5台、列は1本)を比較してみればすぐに分かります。どうぞこのツールで計算してみてください。
【例】
・『平均到着率』を1時間あたり100件
・『平均サービス率』を1時間あたり50件(一つの窓口で処理できる件数)
・『窓口数』を5
とした場合、『窓口ごとに列を作る』と『行列は1本のみ』で比較すると、前者の待ち時間が約5分であるのに対し、後者の待ち時間は約40秒となります。
無料で利用できる『お試しユーザ』では入力パラメータを保存しておくことができませんが、計算自体は何度でも可能です(有料会員はサーバ内に一つだけ各種設定値を保存できます)。
一度『お試しユーザ』でご利用いただき、継続的に利用する価値があると判断していただければ、『会員登録』及び『会費お支払い』をお願い申し上げます(Webサイト運営費用として活用させていただきます)。