Friction River Software - 待ち行列理論の説明（会話風）

Ａ子

いつもいつもこの時間って、何とかならないのかしら？

まさに『長蛇の列』ね

Ｂ美

「うまいこと言った」みたいなドヤ顔は止めてね
たしかに１本の列がぐにゃぐにゃと曲がりくねってて、蛇みたいだけど…

Ｃ菜

Ａ子社長のおっしゃる通りですよ～

昼休みの銀行ATMって、有名ラーメン店の行列くらい大変です～

Ｂ美

少しずつでも前に進んでるんだから良いじゃない

まぁ、こうしてる間にも、私たちの後ろにどんどん人の列が延びてるんだけどね（苦笑）

Ａ子

ところでATMの機械ってここには6台もあるのに、わざわざ列を1本にしてるのはなんで？
ロープまで張っちゃってさぁ

6台のATMそれぞれに並べば良いじゃん

Ｂ美

そのほうが待ち時間が短くなるからよ

Ｃ菜

え？意味が分かりませんよ～

ATMの台数が増えるわけでもないし、人の数が減るわけでもないのに～

Ａ子

あ、分かったわ

列が1本だと、その列ってどうしても長くなるわよね
それを見た利用者がうんざりして並ぶのを止めるから！

どうよ（ドヤ顔）

Ｂ美

うざっ！
ドヤ顔は止めろっつーの

てか、不正解だから！（まぁ、少しはその効果もあるかもだけど…）

Ｃ菜

うーん、分からないです～

わざわざ列を1本にする理由～？

Ｂ美

答えを言っちゃうと、確率論的にそうなるから…

正確には「待ち行列理論」によって明らかになっているから…かしらね

Ａ子

そうこうしているうちに自分の順番が回ってきたわ

この話はまたあとでね

Ｂ美

さてお昼ご飯も食べて、会社に戻ってきたわけだけど、さっきの話の続きね

あなたたちには「待ち行列理論」の基礎の基礎について講義してあげましょう

Ａ子

いや、別に要らない…かな
難しそうだし…

Ｃ菜

私は楽しみですぅ～♪

Ａ子

え？裏切り？裏切りなの？
光秀なの？

Ｃ菜

誰が明智か～！

ここは本能寺じゃありませんよ～

Ｂ美

はいはい、それじゃ始めるわよ

まずは窓口が１個しかない場合ね
あ、ATMで言えば１台しかないって場合よ

Ｃ菜

コンビニのATMって感じですね～

Ｂ美

ATMって、利用者がやってくる間隔はまちまちで、その利用時間もまちまちよね

Ａ子

そりゃそうでしょ

ATMに限らず全ての窓口、えーっと例えばコンビニやスーパーのレジとか、役所の窓口とかもそうなるかな

Ｂ美

なかなか分かってるじゃない
そう、この世にある様々なサービスの窓口は、だいたいそういうものなのよ

さて、それでは利用者のやってくる時間間隔を『Ta』、日本語では『平均到着時間間隔』としましょう。
次に、窓口を利用する時間を『Ts』、日本語では『平均サービス時間』とします。

ここまでは良いかな？

Ｃ菜

大丈夫ですぅ～

Ｂ美

『Ta』の逆数を『λラムダ』として、『平均到着率』
『Ts』の逆数を『μミュー』として、『平均サービス率』と呼称します

要するに、ある時間内にどれだけの人がやってくるかが『λラムダ』で、ある時間内にどれだけの人にサービスを提供できるかが『μミュー』ってことなのよ

Ａ子

だんだんやばくなってきたかも…

えっと、『λラムダ＝１÷Ta』で、『μミュー＝１÷Ts』ってことで良いのかな？

Ｂ美

逆数なんだから当然そうなるわね

あとは、『平均待ち時間』を『Tw』と表記し、これを計算で求めていくわけよ

Ｃ菜

出てくるギリシャ文字はλラムダとμミューだけですか～？

Ｂ美

あと一つだけあるわ

最も重要な『ρロー』、日本語では『窓口利用率』ね
これは「λラムダ÷μミュー」、言い換えれば「μミュー分のλラムダ」で求められるの

Ａ子

ｐピー？

Ｂ美

ρローだっつーてんだろ

まぁ、呼び方はどうでもいいんだけど…
要するに100の能力があるのに、その能力を60しか使ってなけりゃ、ρローは0.6ってことよ

Ｃ菜

えっとぉ～、例えば１時間に40人対応できるレジに30人のお客さんが来たら、ρローは４分の３だから0.75ってことですかぁ～？

Ｂ美

まさにその通り！

その例だと『λラムダ』が30で、『μミュー』が40ってことになるのよ

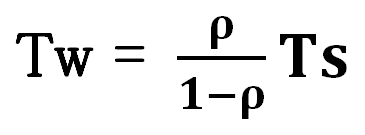
Ｂ美

それじゃ上記の公式にあてはめてみましょう

ちなみに、Tsはμミューの逆数だから40分の1（0.025時間）ってことになるんだけど、さっきの単位は「時間」だったから「分」に換算すると1分半（90秒）ってことになるわね

Ｃ菜

0.75を（1-0.75）で割るとちょうど3ですぅ～
それに1分半を掛けるということは…

分かりました～
待ち時間Twは4分半になりますです～

Ｂ美

正解よ

あ、待ち時間は4分半なんだけど、自分が窓口を利用する時間が1分半だったらそれを足して、トータルで6分ってことになるわね

Ａ子

その列に並び始めてから、終わって出ていくまでの時間が6分ってことか
てかさ、利用率が0.9つまり90%とかだと、Tsの9倍の時間だけ待たされるってことになるじゃん

うーん、計算は簡単だから暗算できそうではあるけどね

Ｃ菜

一人で行列に並んでて、暇なときに頭の中で計算すると良いかもですね～

公式も簡単で憶えやすいです～

Ｂ美

このようにお客さんの到着間隔がばらばらで、かつそれぞれの利用（サービス）時間もまちまちで、窓口数が1個の行列をこう呼ぶの

『M/M/1』の待ち行列と…

Ａ子

えむえむわん？

Ｂ美

そう、M/M/1えむえむわん
余談だけど、この書き方を「ケンドール記号」と呼びます。

では窓口数が2個だったらどうなると思う？
あ、列はそれぞれの窓口ごとに作るとして…

Ａ子

M/M/2えむえむつーね（ドヤ顔）

Ｂ美

ぶっぶー、不正解

Ｃ菜

もしかして、M/M/1が2つあるとかですかぁ～？

Ｂ美

さっすがＣ菜、良い勘してるー
窓口が2個あっても、それぞれに列を作る場合は『M/M/1が2つある』と考えるのよ
もちろん窓口利用率であるρローは2で割るから半分になるわ

あ、でもね、Ａ子の言った『M/M/2』という表現も実は存在するの
それこそが「行列を1本」にした場合なのよ

Ａ子

ん？ということは昼休みの銀行ATMって、M/M/6えむえむしっくすだったってこと？

Ｂ美

大正解！

M/M/1えむえむわんが6個あるよりも、M/M/6えむえむしっくす一つのほうが劇的に待ち時間が少なくなるってこと

Ａ子

うーん、そのへんがどうにも納得しづらい点なのよね

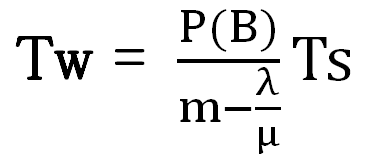
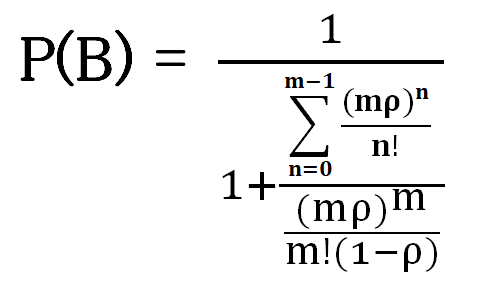
Ｂ美

上記の公式が『M/M/m』（ただしm≧2）の待ち時間を得るものよ

あ、mは窓口数のことね

Ａ子

・・・

Ｃ菜

・・・

Ｂ美

無言になる気持ちはよく分かるわ（苦笑）

こんなのを手計算なんて、とてもじゃないけどやってられないわよね

Ｂ美

ところで、いきなり話は変わるんだけど『FRS統合サービス』ってWebアプリケーションがあるのよね
ここって無料のお試しユーザであっても色々な便利機能を利用できるのよ

とりあえず「ユーザID」と「パスワード」の両方に『guest』と入力してから【ログイン】ボタンを押してみて

Ｃ菜

上から4番目に【待ち行列理論による計算機】というのがあるです～

Ｂ美

出てきた画面に計算したいパラメータを入力してね

うーん、そうね
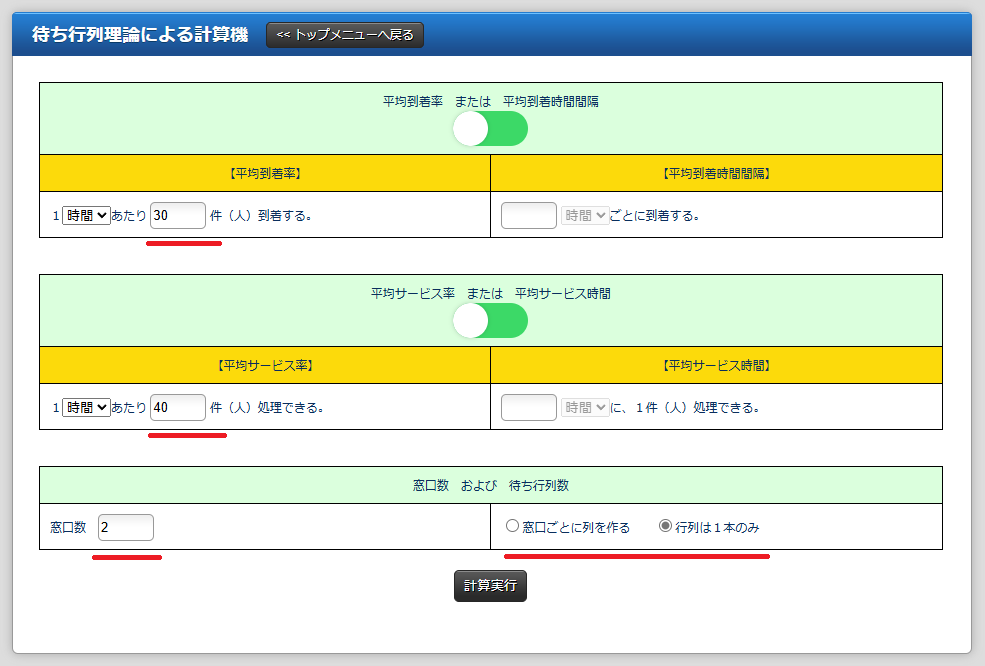
さっきの例で言うと、【平均到着率】を1時間あたり30件、【平均サービス率】を1時間あたり40件にして、「窓口数」を2、「行列は1本のみ」にしてみましょうか

Ｃ菜

【計算実行】ボタンをえいっ！…と押すです～

Ａ子

おぉ！まさに一瞬じゃん

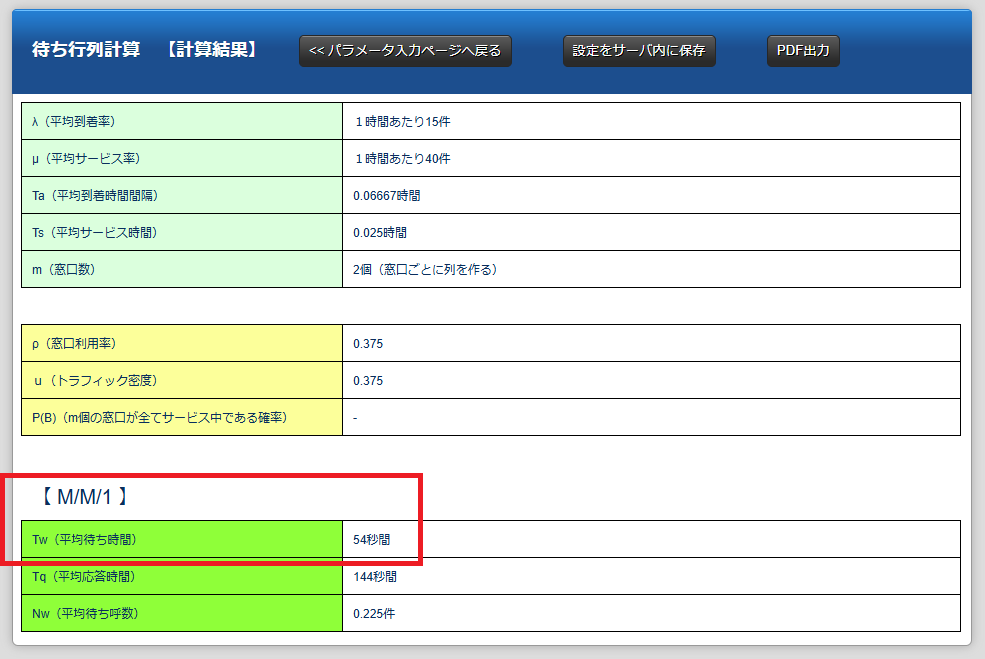
あ、もしも「窓口ごとに列を作る」だったらどうなるの？

Ｃ菜

やってみるです～

Ｂ美

どう？窓口が1個だったら待ち時間（Tw）は4分半、つまり270秒だったわけだけど…

窓口が2個の場合
M/M/1えむえむわんでは待ち時間が半分の135秒になるんじゃなくて、ρローが半分の0.375になるわけ

つまり待ち時間は54秒と、かなり少なくなっていることが分かるわよね

Ａ子

ちょっと待って！

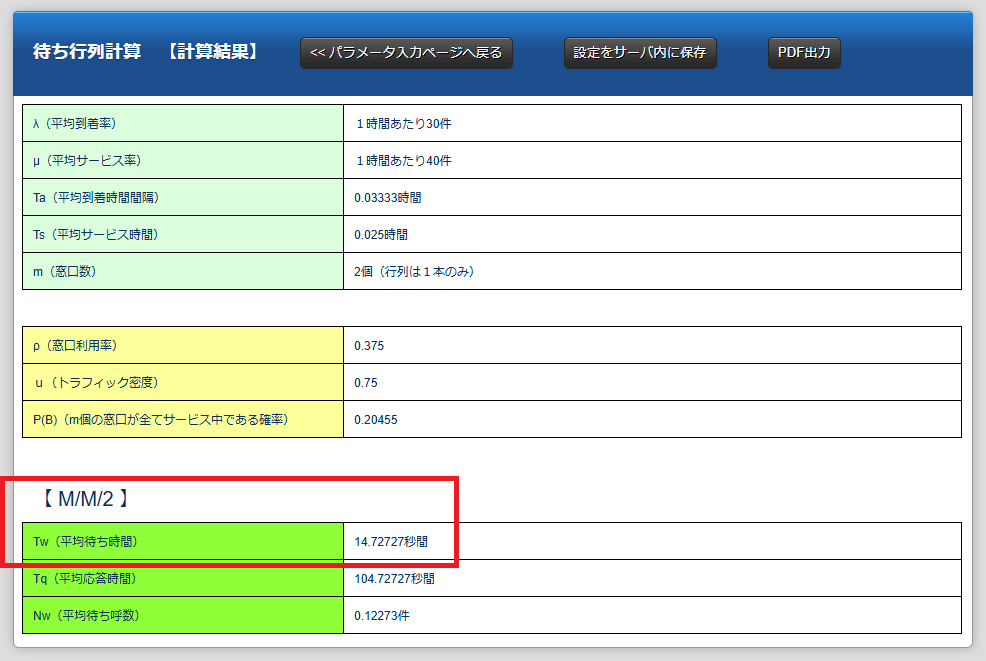
M/M/2えむえむつーの場合の待ち時間を見てよ
なにこの数値、まじ？
ほんとに正しいの？

Ｂ美

もちろん正しいわよ

待ち時間は驚異の約15秒、どうよ（ドヤ顔）

Ａ子

ドヤ顔うっざ

うーん、でも列を1本にするってのが、めちゃくちゃ意味があるってこと、よーく分かったわ
なぜそうなるのかは未だによく分からんけど…

Ｂ美

大丈夫、私も分かってないから（笑）

Ｃ菜

「列を1本にすることに意味がある」ってことを知っていれば良いってことですよね～？

Ｂ美

そういうこと

ちなみに、「待ち行列理論」ってネットワーク技術者エンジニアの必須知識だからね
複数のサーバとロードバランサを組み合わせて『M/M/m』（ただしm≧2）を作ったりするわけ

Ａ子

またわけの分からんことを…（苦笑）